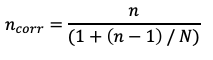Was ist eine repräsentative Stichprobe?

Wenn wir in einer Umfrage Meinungen, Einstellungen, oder Informationen zu Verhaltensweisen abfragen, möchten wir in aller Regel feststellen, wie weit diese Meinungen, Einstellungen und Verhaltensweisen in der Gruppe der Menschen verbreitet sind, die uns interessieren.

Das können zum Beispiel bestehende und/oder potenzielle Kunden eines Unternehmens, seine Mitarbeiter, die Einwohner einer bestimmten Stadt, die vor der Wahl des Bürgermeisters stehen, oder die gesamte Bevölkerung eines Landes sein.

Die Gesamtheit dieser Menschen, deren Meinung uns interessiert, nennt man “Grundgesamtheit”.

In den meisten Fällen ist es allerdings unpraktikabel jeden zu der Grundgesamtheit gehörenden Menschen zu befragen: Abgesehen davon, dass wir nur in den seltensten Fällen jeden einzelnen Menschen aus der Grundgesamtheit kontaktieren und darum bitten können, an unserer Umfrage teilzunehmen, wäre das meistens schlicht und ergreifend zu teuer. Zudem würde eine solche Befragung ziemlich viel Zeit in Anspruch nehmen.

Deshalb setzte sich die Wissenschaft mit der Frage auseinander, ob und inwiefern es möglich ist, nur einige wenige Menschen aus der Grundgesamtheit zu befragen und trotzdem derartige Antworten zu bekommen, die für die Grundgesamtheit charakteristisch – also repräsentativ – sind.

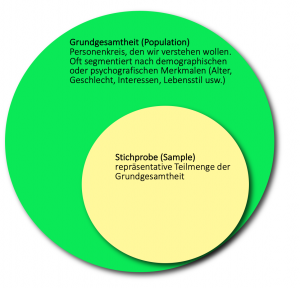
Diese Teilmenge nennt man “Stichprobe”. Analog dazu wie ein Bäcker das Brot an verschiedenen Stellen durchsticht, um festzustellen, ob es gleichmäßig gebacken ist, “stechen” die Statistiker in verschiedene Teile der Grundgesamtheit ein, um festzustellen, ob die Menschen darin ähnlich “gebacken” sind.

Letzten Endes hat die Statistik die Antwort auf diese Frage gefunden und die Antwort war ein klares Jain.

Nein – weil es unmöglich ist, anhand einer Stichprobe auf genau dieselbe Antwort zu kommen, die bei der Befragung der kompletten Grundgesamtheit der Fall gewesen wäre.

Ja – weil es mit Hilfe der Wahrscheinlichkeitsrechnung möglich ist einzuschätzen, wie stark der echte Wert (z.B. Durchschnittseinkommen, oder Anteil derjenigen, die das Produkt X präferieren) in der Grundgesamtheit von dem mit Hilfe der Stichprobe ermittelten Wert abweichen kann. Mit anderen Worten es ist möglich das Intervall einzuschätzen, in dem der echte Wert höchstwahrscheinlich liegt.

Die Voraussetzungen dafür, dass dieser Intervall berechnet werden kann, sind

• Zufällige Stichprobenziehung. D.h. jeder Mensch aus der Grundgesamtheit hat dieselbe Chance in die Stichprobe zu gelangen.
• Es muss eine bestimmte Mindestanzahl von Menschen (Stichprobengröße) befragt werden

Sind diese beiden Voraussetzungen erfüllt, so gilt die Stichprobe als repräsentativ für die Grundgesamtheit. Die mit Hilfe einer solchen Stichprobe gewonnenen Erkenntnisse können wir auf die Grundgesamtheit übertragen und die Wahrscheinlichkeit angeben, mit der wir uns sicher sind, dass wir dabei keinen Fehler machen.

Wie die Stichprobengröße berechnet wird und wie Sie die Stichprobengröße selbst berechnen können, erklären wir in dem nächsten Abschnitt.

Was passiert wenn die Stichprobengröße falsch gewählt wird?

Die Folgen einer falschen Auswahl der Stichprobengröße sind denkbar einfach:

• Ist die Stichprobe zu klein, so können wir die Umfrageergebnisse nicht auf die Grundgesamtheit verallgemeinern bzw. die Parameter in der Grundgesamtheit nicht mit der gewünschten Präzision einschätzen.
• Ist die Stichprobe zu groß, so schadet es zwar den Ergebnissen nicht, die Kosten der Datenerhebung können aber höher ausfallen, als es notwendig gewesen wäre. Besonders spürbar wird es bei der Verwendung von Panels, wobei jeder Proband mehrere Euros kostet.

Der Ansatz der Fehlerspanne zur Berechnung der Stichprobengröße

Wannimmer wir basierend auf der Stichprobe Aussagen über die Grundgesamtheit treffen, machen wir einen Fehler. Dieser Fehler resultiert daraus, dass wir nicht die komplette Grundgesamtheit sondern nur einen Teil davon befragen.

Sofern die Stichprobe zufällig gezogen wurde, können wir diesen Fehler mit Hilfe der Wahrscheinlichkeitsrechnung berechnen und den Bereich angeben, in dem sich der wahre Wert (z.B. der Anteil von Menschen, die eine Frage auf bestimmte Weise beantworten) in der Grundgesamtheit befindet.

Dieser Bereich nennt sich Konfidenzintervall und ergibt sich als “gemessener Wert +/- Fehlerspanne”.

Die Formel zur Berechnung der Fehlerspanne (für unendlich große Grundgesamtheit) sieht wie folgt aus:

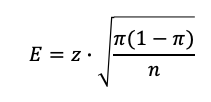(1)

hier,

E – Fehlerspanne (in Prozent, ausgedruckt in Dezimalzahlen).

z – Die Differenz zwischen dem in der Stichprobe beobachteten Wert und seinem theoretischen Mittelwert, die für das vorgegebene Vertrauensniveau maximal zulässig ist.

Z-Wert gibt somit im Grunde die Breite des Konfidenzintervalls vor, tut es allerdings in Begriffen der Anzahl von Standardabweichungen der Standardnormalverteilung. Alle restlichen Parameter der Formel dienen lediglich dazu, den z-Wert in die verständlichere und einfach interpretierbare Einheiten der maximal zulässigen prozentualen Abweichung zu übersetzen.

Z-Wert für verschiedene Vertrauensniveaus kann mit Hilfe der sogenannten z-Tabelle ermittelt werden.

In der Umfrageforschung werden typischerweise folgende Vertrauensniveaus bzw. ihnen entsprechende z-Werte verwendet:

Vertrauensniveau	z-Wert
90%	1,65
95%	1,96
99%	2,58

Höheren Vertrauensniveaus entsprechen höhere z-Werte. Deshalb wird auch die Fehlerspanne für höhere Vertrauensniveaus höher.

π – Anteil des Merkmals in der Grundgesamtheit (in Prozent, ausgedruckt in Dezimalzahlen). Der π-Wert kann also zwischen 0% und 100% variieren.

In der Regel ist der π-Wert im Vorfeld einer Umfrage nicht bekannt. In solchen Fällen setzt man ihn auf 50% (0,5). Das ist deshalb so, weil der Ausdruck π(1 – π) seinen Maximum bei π = 0,5 hat, was in den höchsten E-Wert für alle mögliche Werte von π resultiert. Das gewährleistet, dass selbst in ungünstigen Fällen, das ermittelte Konfidenzintervall den wahren Wert einschließt, oder dass eine ausreichend große Stichprobe generiert werden kann.

Werte von π, die von 0,5 nach oben oder nach unten abweichen, produzieren kleinere Fehlerspannen. Bei π = 0 und π = 1 ist die Fehlerspanne = 0.

Wenn Sie also vor der Durchführung Ihrer Umfrage den Anteil des Sie interessierenden Merkmals in der Grundgesamtheit wissen, können Sie die Fehlerspanne – und wie wir es später zeigen werden, auch die erforderliche Stichprobengröße – deutlich reduzieren, indem Sie diese Information berücksichtigen.

Beispiel:
In Ihrer Studie untersuchen Sie die Frage, welcher Anteil der Schüler ein eigenes Laptop besitzt. Da darüber im Hinblick auf die von Ihnen definierte Grundgesamtheit noch nichts bekannt ist, nutzen Sie den Wert π = 0,5. Es stellt sich heraus, dass 67,5% der Befragten diese Frage bejaht haben. Sie wiederholen die Studie mit der gleichen Grundgesamtheit und nutzen nun den Wert π = 0,675, was den notwendigen Stichprobenumfang verringert.

n – Anzahl der befragten Personen, also Stichprobengröße.

Nachdem wir uns mit der Bedeutung aller Parameter in der Formel für die Berechnung der Fehlerspanne auseinandergesetzt haben, ist es einfach zu sehen, dass wir dieselbe Formel zur Berechnung der Stichprobengröße verwenden können. Dafür bedarf es einiger Umstellungen. Die resultierende Formel für die Berechnung der Stichprobengröße sieht danach so aus:

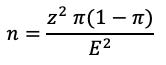(2)

Die Vorgehensweise für die Berechnung der Stichprobengröße ist nun ganz einfach:

1. Wähle die Fehlerspanne aus, die für die Umfrageergebnisse gelten soll.
2. Wähle das Vertrauensniveau aus, für das die Ergebnisse der Umfrage gelten sollen.
3. Ermittle den z-Wert, der dem gewählten Vertrauensniveau entspricht.
4. Ist der Anteil des interessierenden Merkmals in der Grundgesamtheit bekannt, so nutze ihn als π. Ist das nicht der Fall, setzer π = 0,5.
5. Setze die Werte in die Formel (2) ein und rechne die Stichprobengröße sie aus.

Somit haben Sie die Stichprobengröße für den Fall der unbekannten oder unendlich großen Grundgesamtheit ermittelt.

Stichprobengröße für endliche Grundgesamtheit

Es stellt sich heraus, dass in Fällen, wenn die notwendige Stichprobengröße vergleichbar mit dem Umfang der Grundgesamtheit wird, bereits kleinere Stichprobengrößen für die Repräsentativität der Umfrageergebnisse ausreichen.

In diesem Fall wird die von der Stichprobe nicht erfasste Varianz des Merkmals vergleichbar mit der erfassten Varianz, sodass die Fehlerspanne um den sog. Finite Population Correction (FPC) Faktor nach unten korrigiert werden kann:

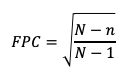(3)

wobei N für die Größe der Grundgesamtheit steht.

Die Formel zur Berechnung von Fehlerspanne nimmt dabei folgende Form an:

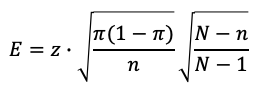(4)

Der wert von FPC kann zwischen 0 und 1 Variieren.

Je näher die Stichprobengröße (n) an den Umfang der Grundgesamtheit (N) ist, desto kleiner wird FPC. Folglich fällt auch die Fehlerspanne kleiner aus.

Je kleiner der Stichprobenumfang im Vergleich zur Größe der Grundgesamtheit ist, desto näher an die 1 wird der Wert von FPC. Somit verliert der FPC-Faktor an Bedeutung und die Formel (4) artet sich zu der Form (1) aus.

Die Formel für die Berechnung der Stichprobengröße mit Berücksichtigung von FPC sieht nach der Auflösung von Formel (4) nach n so aus:

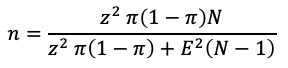(5)

Der Umfang der Stichprobengröße kann in diesem Fall analog zu der im vorherigen Abschnitt erläuterten Vorgehensweise berechnet werden:

1. Man ermittle die Werte für E, z, π und N.
2. Setze sie in die Formel (5) ein.
3. Berechne die notwendige Stichprobengröße.

Alternativ und besonders hilfreich bei händischer Berechnung kann man auch wie folgt vorgehen:

1. Berechne die Stichprobengröße für unendliche Grundgesamtheit – nach Formel (2).
2. Wenn die berechnete Stichprobengröße mehr als 5% (spätestens aber größer als 10%) der Grundgesamtheit beträgt, berechne die korrigierte Stichprobengröße nach der Formel
   

   (6)

   n_corr ist der notwendige Stichprobenumfang.

Beispiel:
Wir führen eine Mitarbeiterumfrage durch, die repräsentativ für das gesamte Unternehmen mit der Fehlerspanne von 5% und Vertrauensniveau von 95% sein soll. Nach der Formel (2) berechnen wir die notwendige Stichprobengröße:

n = (1,96^2 * 0,5* 0,5)/ 0,05^2 = 385.

In unserem Unternehmen arbeiten jedoch nur 100 Mitarbeiter. Somit ist die Korrektur der Stichprobengröße notwendig. Deshalb berechnen wir die korrigierte Stichprobengröße nach Formel (6):

n_corr = 385 / (1 + ( 385 – 1)/100) = 80.

Im Endeffekt müssen wir 80 Mitarbeiter befragen, damit die Umfrage als repräsentativ für alle Mitarbeiter unseres Unternehmens gelten kann.